In most species mRNAs are purine-loaded in regions with the potential to form loops in stem-loop secondary structures (Szybalski et al. 1966; Smithies et al. 1981; Bell and Forsdyke 1999a,b). Like GC-pressure and fold (stem-loop) pressure, the pressure to purine-load (AG-pressure) can affect the amino acid composition of proteins (Forsdyke and Mortimer 2000). Whereas selective forces promoting the development of GC and fold pressures are likely to operate primarily at the genomic level (Grantham 1980; Bernardi and Bernardi 1986; Forsdyke 1996, 1998, 1999; Barrette et al. 2001; Knight et al. 2001), it is proposed that selective forces for the development of AG-pressure operate primarily at the non-genomic level. A general purine-loading of loops in mRNA secondary structures would militate against unwanted mRNA-mRNA interactions (Bell and Forsdyke 1999b) and the formation of segments of "self" double-stranded RNA of a length sufficient to trigger intracellular alarms. Pressure to purine-load provides a possible explanation for apparently non-functional low complexity (simple sequence) elements in proteins of the malaria agent Plasmodium falciparum (Pizzi and Frontali 2001; Forsdyke, 2002b; Xue and Forsdyke 2003), and of viruses (Cristillo et al. 2001).

   Being largely entropy-driven (Lauffer 1975; Cantor and Schimmel 1980), RNA-RNA interactions should increase with temperature. Thus, the need to prevent unwanted interactions might be greater in organisms that normally grow at high temperatures, or are periodically exposed to such temperatures. Consistent with this, in a previous study of a small number of prokaryotes for which extensive genomic sequences were available, purine-loading was found to be greatly increased in thermophiles to an extent sufficient to influence amino acid composition (Lao and Forsdyke 2000). This was confirmed in a recent study with 25 completely sequenced genomes (Lobry and Chessel 2003). We have now extended our study to a much larger number of prokaryotic species for which sequence information, albeit often limited, is available. We have also examined the responsiveness of bases in different codon positions to AG-pressure and the relationship of AG-pressure to GC-pressure. Our results have implications for understanding how nucleic acids maintain active configurations at high temperatures, and how forces other than those of conventional Darwinian natural selection can influence protein evolution (Hurst and Merchant 2001; Forsdyke 2001a,b; 2002a,b).

Optimum growth temperatures

     A table of optimum growth temperatures was obtained from the German Collection of Microorganisms and Cell Cultures (DSMZ, Braunschweig). Direct examination of the primary literature supported the accuracy of the temperatures in twenty randomly selected cases, so the general accuracy of the table was assumed.

Sequences

    Sequences from the September 2000 release of GenBank have been used to generate "Codon Usage Tables from GenBank" (CUTG; Nakamura et al. 2000). Programs for Microsoft Excel were written in Microsoft Visual Basic for Applications to calculate open reading frame (ORF) base compositions from the CUTG data. We excluded organisms for which there had not been available sequences of at least four ORFs and 2500 bases. The CUTG database had not been screened for redundancies; thus, while the sequence of Escherichia coli K12 contributed approximately 4300 ORFs, under this heading there are 14780 ORFs in the database, implying at least three independent genome equivalents had been used to derived the 64 codon usage values for the species. While this might have introduced some bias, each of the prokaryotic species studied is represented by only one data point in our plots. Thus E. coli with 14780 ORFs has the same representation as a genome for which there are only four ORFs in GenBank. There are reasons why certain species are chosen for sequencing and why certain ORFs are sequenced first; these may not be representative of the corresponding genome. Furthermore, some species are closely related phylogenetically, whereas others are more distantly related. However, the large number of species studied makes it likely that biases would cancel out to permit a fair general picture. Indeed, a recent comparison of datasets from completely sequenced and partially sequenced bacterial genomes gave similar results (Lobry and Chessel 2003).

Chargaff difference analysis

   Violating Chargaff's second parity rule (Forsdyke and Mortimer 2000; Forsdyke 2002a), Chargaff differences (ΔW, ΔS) are the differences between the numbers of the classical Watson-Crick pairing bases in a single-stranded nucleic acid segment ("AT-skew", "GC-skew"). The sign of the differences depends on the direction of subtraction, which in some previous work was determined alphabetically, but in the present work is determined by subtracting the number of pyrimidines (Y) from the number of purines (R). Thus, purine excesses (R>Y) score positively and pyrimidine excesses (R<Y) score negatively.

     Chargaff differences may be calculated as A-T, and as G-C, where A, T, G and C can be the frequency of each base in 1 kb sequence windows. This approach makes no assumption about the disposition of ORFs, and can be applied to uncharted DNA. When an unknown ORF is located, values for windows whose centres overlap the ORF can be averaged to obtain an approximate value for that ORF. For the importance of 1 kb window sizes and other details see Bell and Forsdyke (1999a).

    If the ORFs in a sequence are known, ΔW and ΔS in bases/kb may be calculated either directly from ORF base compositions, or, indirectly, from codon-usage tables. Then ΔW = 1000[(A-T)/N], and ΔS = 1000[(G-C)/N], where N is the total number of bases in an ORF. These two values can be summed to obtain a value for the purine-loading index (i.e. ΔW + ΔS = PLI). This approach disregards non-coding DNA. To distinguish bases in different codon positions, base letters are followed by codon positions. For example, whereas T refers to the quantity of bases in all three codon positions, T1, T2, and T3 refer to the quantities of T in first, second and third codon positions, respectively. Accordingly, the contribution of first codon positions to the W-base component of the Chargaff difference, ΔW1, would be 1000[(A1-T1)/N1].

     It should be noted that (G+C)% (a measure of "GC-pressure") is assessed as the sum of G + C in a sequence, whereas Chargaff differences (a measure of "purine-loading pressure" or "AG pressure") are assessed as the excess of the R bases over the Y bases. Although it might be preferable to assess GC-pressure and AG-pressure in the same way (bases/kb), we here retain the classical measure of GC-pressure (G+C)% (i.e. bases/0.1 kb).

Statistics

     First-order linear regression analyses were performed with the assumption that data points were normally distributed. The probability that the slopes of two regression lines were not significantly different from each other was calculated using an interaction model with dummy qualitative variables as described previously (Forsdyke 1998).

Optimum growth temperature, (G +C )%, and PLI

    We found 550 prokaryotic species for which optimum growth temperatures were known and for which there were at least 4 ORFs and 2500 bases in GenBank. The average number of ORFs was 144+ or -34. 92 species had less than 6 ORFs. 190 species had less than 10 ORFs. Optimum growth temperatures ranged from 17oC (Renibacterium salmoninarum) to 105oC (Pyrodictium occultum). Of the 550 species, 494 had temperature optima below 60oC, and 56 had temperature optima of 60oC and higher.

Fig. 1. Variation of (a) ORF G+C, and (b) ORF PLI with the temperature required for optimal growth. The least squares regression lines for the 550 prokaryotic species studied extend to the Y-axis. Y₀, value for intercept at the Y-axis; Sl, slope with associated probability (P) that the slope is not significantly different from zero; r², adjusted square of the correlation coefficient (i.e. the coefficient of determination). Regression lines for the 494 species with temperature optima <60oC, and for the 56 species with temperature optima of 60oC and greater, are shown as short lines, which do not extend to the Y-axis. Data from this figure are included in Table 1.

    Although the wide scatter of data points indicates other variables affecting base composition, linear regression plots show that the optimum growth temperature of prokaryotes is inversely related to ORF (G+C) percentages (Fig. 1a), and directly related to ORF PLIs (Fig. 1b). In both cases, the greatest response to growth temperature occurs much below 60oC, whereas there is no significant further response over the higher temperature range (i.e. over the higher temperature range P values for local slopes were 0.26 and 0.23 for Figs. 1a and 1b, respectively). The average (G+C)% for prokaryotes with optima below 60oC (52.0 + or - 0.6), was greater (P = 0.002; unpaired t-test) than that for prokaryotes with optima of 60oC and higher (46.6 + or - 1.2). The average PLI for prokaryotes for optima below 60oC (44.4+ or -2.5) was less (P < 0.00001) than that for prokaryotes with optima of 60oC and higher (116.3 + or - 6.0). Thus, effects of growth temperature tend to plateau between 37oC and 60oC.

Table 1. Parameters of linear regression plots for relationship of (G+C)% and PLI to optimum growth temperature

(G+C)% versus temperature

PLI versus temperature

Temperature range

<60^o

60^o +

17^o-105^o

<60^o

60^o +

17^o-105^o

Codon Positions

All^a

Y₀

82.5

38.6

58.5

-96.1

75

-15.4

Slope

-0.95

0.10

-0.19

4.37

0.54

1.83

P^b

<0.0001

0.26

<0.0001

<0.0001

0.23

<0.0001

r²

0.152

0.006

0.052

0.160

0.009

0.211

First

Y₀

78.4

51.3

62.3

67.9

242.8

183.7

Slope

-0.65

0.02

-0.15

5.86

1.23

2.20

P

<0.0001

0.731

<0.0001

<0.0001

0.088

<0.0001

r²

0.149

<0.001

0.063

0.162

0.035

0.174

Second

Y₀

55.0

39.5

45.6

-154.2

22.4

-66.3

Slope

-0.42

-0.03

-0.12

3.61

-0.44

0.84

P

<0.0001

0.437

<0.0001

<0.0001

0.400

<0.0001

r²

0.131

<0.001

0.095

0.086

<0.0001

0.039

Third

Y₀

114.2

25.2

67.7

-202.0

-40.2

-163.7

Slope

-1.77

0.32

-0.31

3.64

0.84

2.45

P

<0.0001

0.087

<0.0001

<0.0001

0.246

<0.0001

r²

0.144

0.036

0.036

0.048

0.007

0.166

aData correspond to Figure 1.

^bProbability that the slope is not significantly from zero. For probabilities that slopes are significantly different from each other, please see text.

    The data of Figure 1 are for bases in all codon positions. Table 1 shows that for some codon positions there is a tendency for progressive effects of growth temperature at temperatures above 60oC. The third codon position is most responsive to temperature in the case of (G+C)% (i.e. for the entire temperature range the slope value of -0.31 for third codon positions is significantly different from the values of -0.15 and -0.12 for first and second codon positions; P = 0.024 and 0.007, respectively). In contrast to the trend at lower temperatures, in the temperature range above 60oC the third codon position (G+C)% shows a slight increase (a positive slope value of 0.32), which is of marginal significance (P = 0.087).

    On the other hand, the first and third codon positions are most responsive in the case of the PLIs. For the entire temperature range, the slope values of 2.20 and 2.45, respectively, while not significantly different from each other (P = 0.43), are both significantly different from the value for second codon positions (0.84; P<0.0001). For the temperature range above 60oC the first position PLI tends to continue the positive relationship with growth temperature observed at lower temperatures (slope 1.23; P = 0.088).

    The PLI has contributions from the W bases (ΔW = A - T) and from the S bases (ΔS = G - C). These contribute approximately equally to the increase of PLI with optimum growth temperature. Thus, over the entire range of optimum growth temperatures ΔW and ΔS values increase with temperature (slopes of 0.88 and 0.95, respectively, which are not significantly different from each other; P = 0.59; data not shown).

 Relationship between (G+C)% and PLI for ORF DNA for 494 prokaryotic species with temperature optima <60oC (open circles; regression line continuous), and for the 56 species with temperature optima of 60oC and greater (closed circles; regression line dashed). Single base letters in bold at the corners indicate quadrants enriched for particular bases [e.g. at high values of (G+C)% and low values of PLI, there is enrichment for C]. The slopes of the regression lines are not significantly different (P=0.30).

    As expected from the above, Figure 2 shows that (G + C)% and PLI are inversely related. Adjusted coefficients of determination indicates that 59% of the variation in (G+C)% relates to the increase in the PLI in the case of species with temperature optima below 60oC (open circles), and 50% of the variation in (G+C)% relates to the increase in the PLI in the case of species with temperature optima of 60oC and higher (filled circles).

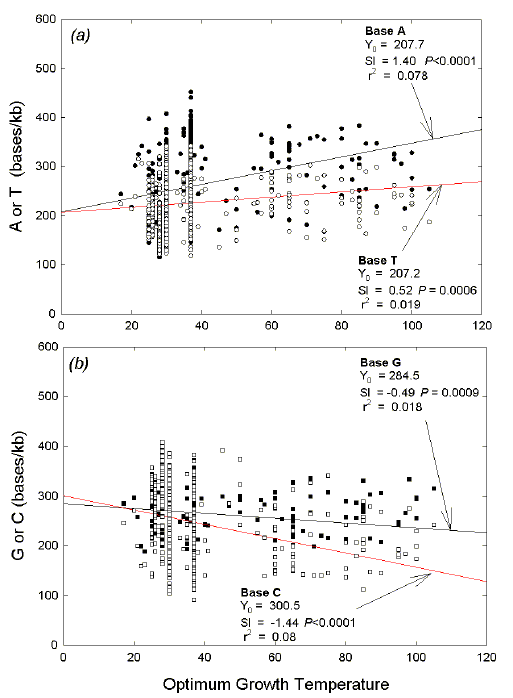
Fig. 3. Variation of base density in ORF DNA with the temperature require for optimal growth of 550 prokaryotic species. (a) The W bases: A, filled circle; T, open circle. (b) The S bases: G, filled square; C, open square. Data in the figure show that all slope (Sl) values are significantly different from zero (P = 0.0009 and less). In addition, slope values for members of each pair are significantly different from each other in (a) P = 0.0005, and in (b) P = 0.0001.

Contributions of individual bases to ΔW and ΔS

     Individual bases contributed in different ways to the observed changes in ΔW and ΔS in response to increased optimum growth temperature. Fig. 3 shows that the increase in ΔW is derived mainly by an increase in ORF content of A, while T remains relatively constant. On the other hand, the increase in ΔS is derived mainly from a decrease in C, while G remains relatively constant. In essence, as temperature increases, A is traded for C.

    In each of Figures 3a and 3b, the regression lines begin to diverge at low growth temperatures. Thus, at the first codon position, purines are in excess even at low temperatures, and this difference further increases as optimum temperature increases. Accordingly, a distinction can be made between a base-line contribution to purine-loading, and a response to a further pressure to purine-load, in the present case arising from an increase in growth temperature. 

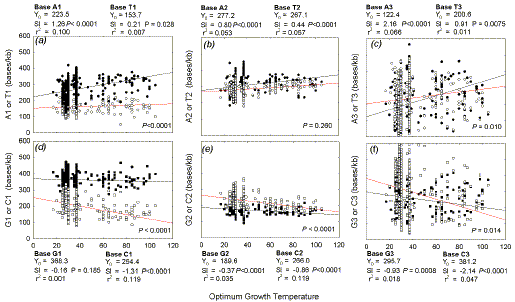
 Variation of base density in different codon positions with the temperature required for the optimal growth of 550 prokaryotic species. Linear regression parameters shown outside the figures are as in Figure 1. The probabilities that the slopes of the two lines in each figure are not significantly from each other are shown within the figure. For other details see Figure 3.

    Fig. 4 shows that, while A-for-C trading is true for all codon positions, the major contribution to ΔW and ΔS is in the first codon position. However, the major response to increasing optimum growth temperature is in the third codon position (greatest positive slope for A, and greatest negative slope for C).

    The difference between the slopes for each pair of Chargaff bases is highly significant in the case of first codon positions (Figs. 4a, d; P<0.0001), and second codon position S bases (Fig. 4e; P <0.0001). The difference is significant in the case of third codon positions, but here purines do not exceed pyrimidines until 63oC (W bases; Fig. 4c) and 71oC (S bases; Fig. 4f). There is no significant increase in second codon position ΔW with growth temperature (Fig. 4b), although purines are generally in excess of pyrimidines. There is symmetry in positive and negative slope values for the non-Watson-Crick base pairs (A and C; T and G), which is particularly apparent in third codon positions (e.g. A3, 2.16; C3, -2.14; T3, 0.91; G3, -0.93).

Table 2. Average ORF Base Densities^a at Low or High Growth Temperatures

Base and Codon
Position

Optimum Growth Temperature

(degrees Celcius)

<60^b

60+^c

Difference

P^d

A1

265.7

+ or -2.6

304.3

+ or -6.0

38.6

<0.00001

C1

210.8

+ or -2.5

166.6

+ or -5.8

-44.2

<0.00001

G1

362.5

+ or -1.9

363.9

+ or -4.8

1.4

0.802

T1

161.1

+ or -1.5

165.1

+ or -4.5

4.0

0.400

A2

304.4

+ or -2.3

325.1

+ or -4.5

20.7

0.004

C2

237.8

+ or -1.6

203.7

+ or -3.2

-34.1

<0.00001

G2

176.6

+ or -1.3

169.3

+ or -2.5

-7.3

0.073

T2

281.2

+ or -1.2

301.9

+ or -2.8

20.7

<0.00001

A3

194.7

+ or -5.5

260.9

+ or -14.0

66.2

0.00013

C3

309.5

+ or -6.6

244.0

+ or -14.8

-65.5

0.00127

G3

262.8

+ or -4.5

250.9

+ or -10.6

-11.9

0.390

T3

233.0

+ or -5.5

244.1

+ or -11.7

11.1

0.510

d Unpaired t-test.

    In Table 2 average values for base densities for the 494 species with growth optima less than 60oC are compared with the corresponding average values for the 56 species with growth optima of 60oC and higher. First and third codon positions show major gains in A and declines in C, but small changes in G and T, which are not statistically significant. For second codon positions the most significant changes are in the pyrimidines. A significant increase in the purine A is countermanded by a decrease in the purine G.

PLI is positively related to growth temperature

    The previously reported positive correlation of purine-loading with optimum growth temperature (Lao and Forsdyke 2000) is here confirmed for a much larger sample of prokaryotes (Fig. 1b). Data from eukaryotes are limited. Our preliminary studies show that the heat-tolerant marine worm Alvinella pompejana (Sicot et al. 2000) has much more purine-loading of its mRNA than comparable mesophilic worms. Among 51 chloroplast genomes, species at the upper extreme of the distribution of PLI values include the thermophiles Astasia longa (PLI = 126 bases/kb for 37 sequenced ORFs) and Galeria sulphuria (PLI 124 bases/kb for 9 sequenced ORFs). However, while the generalization that thermophiles usually have purine-loaded mRNAs is supported, the converse does not apply. High purine-loading is found in some mesophilic species (Fig. 1b).

    While not excluding other causes of high purine-loading, such as low GC-pressure (see below) or an inability to escape usage of purine-rich codons ("protein pressure"), it is possible that purine-loading in non-homeothermic organisms reflects intermittent exposure to high temperatures. This might apply to organisms living in the surface layers of tropical soil (e.g. the 24 Clostridial species in GenBank represented by at least 4 ORFs and 2500 bases have an average PLI of 144 bases/kb).

    It should also be noted that pyrexia, an elevation in temperature that constitutes part of the adaptive response to pathogens (Forsdyke 1995), is achieved by behavioural adaptation in organisms not able to regulate body temperature physiologically (e.g. they migrate to full sunlight). If one of the hosts of a pathogen were non-homeothermic and could elevated its temperature to high levels behaviourally, then that pathogen might have purine-loaded mRNAs, many of which might also be expressed in an alternative homeothermic host. In this light we can interpret high purine-loading in genera such as Borrelia, the agent of tick-borne infections (8 species in GenBank have an average PLI of 140 bases/kb), and in Plasmodium falciparum (Pizzi and Frontali 2001; Forsdyke, 2002b; Xue and Forsdyke 2003). In a preliminary study of viruses of the genus Flavivirus we find non-vector-borne viruses to have less purine-loading than vector-borne viruses, but to show little difference in (G+C)% (c.f. Jenkins et al. 2001).

(G+C)% is negatively related to growth temperature

    Since rRNAs and tRNAs function by virtue of their structures rather than by virtue of encoding information for a protein, and since the maintenance of those structures should be required for function at high temperatures, it is not surprising that the (G+C)% contents of these RNA species increase with optimum growth temperature (Forterre and Elie 1993; Dalgaard and Garrett 1993; Galtier and Lobry 1997). However, mRNAs might not be so constrained. Their structures, which can appear just as elaborate as those of rRNAs, probably reflect pressures that operate at the genomic level on both genic and non-genic DNA (e.g. to assist recombination; Forsdyke and Mortimer 2000; Forsdyke 2001a; Barrette et al. 2001).

    Our observation that ORF (G+C)% is decreased in prokaryotes with high optimum growth temperatures suggests that such genomic operations, even while requiring secondary structure, can occur at high temperatures without the need for a (G+C)% increase. This is in agreement with Hurst and Merchant (2001), who conclude that "within prokaryotes GC content in protein-coding genes, even at relatively freely evolving sites, cannot be considered an adaptation to the thermal environment." Similarly, Ream et al. (2003) note for a variety of vertebrate species no change in the (G+C)% of specific genes as a function of average species temperature over the range -1.86oC (fish) to 45oC (desert reptile). Adaptations to facilitate genomic operations in thermophiles would include high intracellular concentrations of K⁺ and other cations, relaxation of supercoiling, and association with polyamines and specialized DNA-binding proteins (Forterre and Elie 1993; Stetter 1999; Bernardi 2000; Forsdyke and Mortimer 2000; Grove and Lim 2001).

    Although we assessed the (G+C)% content only of ORFs, these comprise such a large part of prokaryotic genomes that our data are likely to reflect total genomic (G+C)%. However, in contrast to our results (Fig. 1a), values for (G+C)% derived from buoyant density centifugation and thermal denaturation profiles demonstrate no correlation between the genomic G+C content and optimal growth temperature in prokaryotes (Forterre and Elie 1993; Galtier and Lobry 1997). The latter authors have interpreted their data as supporting a neutralist (non-selectionist) view of the cause of variations in genome base composition at   "freely evolving sites" (Hurst and Merchant 2001), and as opposing our proposal that the ubiquitous occurrence of stem-loop potential in genomes is of adaptive value. Both these interpretations are disputed (Forsdyke and Mortimer 2000; Forsdyke 2002b).

(G+C)% is negatively related to PLI

    The general nature of the inverse relationship between PLI and (G+C)% noted previously in prokaryotes (Lao and Forsdyke 2000) and eukaryotes (Saccone et al. 2000; Cristillo et al. 2001) is confirmed in the present work (Fig. 2). Individual codons of a particular amino acid can be differentially affected by the two pressures. Thus, the frequency of arginine codon CGC increases progressively with increasing (G+C)%, but the frequency of arginine codon GCA remains constant, indicating that here the pressure for A to decrease balances the pressure for G and C to increase (Knight et al. 2001). The latter authors conclude that "codon and amino-acid usage is consistent with forces acting on nucleotides rather than on codons or amino acids" (our italics; see Grantham 1980).

    Under what circumstances AG-pressure would respond to GC-pressure, or vice versa, remains to be determined. By the mechanism we have proposed, an evolutionary chain of causation would be: (i) elevation of temperature; (ii) increased purine-loading; (iii) decrease of (G+C)%. The latter decrease would be secondary to the primary adaptation of purine-loading, and hence would be an indirect adaptation to a thermal environment.

    It should be noted that increased AG-pressure per se does not imply a decrease in (G+C)%. Trading As for Ts would purine-load without affecting (G+C)%. Trading Gs for Ts would increase the (G+C)%. The decrease implies a preference for trading As for Cs, perhaps because this would minimize the amino acid miscoding penalty. Codon flexibility in this respect is most in third codon positions and least in second codon positions. According to the RNY rule for average codon composition (Eigen and Schuster 1978; Shepherd 1981), the first codon position is already R-rich in species with low optimum growth temperatures, so that, while adept at receiving more A (slope value of 1.26; Fig. 4a), it is not as adept at receiving more A as is the third codon position, which is Y-rich in species with low optimum growth temperatures. Thus, A3 responds dramatically to increased optimum growth temperature and has a slope value of 2.16 (Fig. 4c). Being Y-rich, the third codon position is also particularly adept at donating C. Thus, C3 has a slope value of -2.14 (Fig. 4f).

    The tendency to decrease C in thermophiles would mean there would be less C at risk of deamination at high temperatures. However, A-for-C trading is also observed in plots of base composition against (G+C)% for the 1046 prokaryotic species and 161 bacteriophage species that fulfill our selection criteria (at least 4 ORFs and 2500 bases in GenBank). For many of these, optimum growth temperatures are not available; however, as (G+C)% increases, A decreases and C increases, apparently irrespective of the optimum growth temperature (Mortimer and Forsdyke 2003).

Nucleic acid constraints on phenotype

     Since second codon positions are of major importance in determining the encoded amino acid, the trading of C2 predicts, for example, that serines (with codons UCN ) will be replaced in thermophiles by other amino acids, or will be encoded by purine-loaded codons for serine (AGY). Thus, because the amino acid composition of thermophile proteins is different from that of mesophile proteins, it should not be concluded that such changes are necessarily adaptive with respect to protein function at high temperatures (Lao and Forsdyke 2000; Lobry and Chessel 2003). Since decreased (G+C)% correlates with an increase in hydrophilic, charged, amino acid residues (D'Onofrio et al. 1999), and since (G+C)% and PLI are reciprocally related (Fig. 2), then thermophiles, by virtue of their high purine-loading, should have proteins rich in charged residues (Lys, Arg, Glu). These might indeed aid protein stability and militate against protein aggregation (Jaenicke and Bohm 1998; Cambillau and Claverie 2000), but it should be noted that the corresponding codons are often purine-rich.

    Like GC-pressure (Knight et al. 2001), AG-pressure has the potential to influence the amino acid content of proteins, and hence protein-dependent aspects of the phenotype. AG-pressure appears to affect preferentially nucleic acid segments encoding low-complexity regions of proteins, possibly surface-located (Fukuchi and Nishikawa 2001). It is proposed that sometimes such regions exist, not because of a function required at the protein level, but to permit purine-loading of the corresponding nucleic acid without compromising protein functional domains. Thus, proteins may be larger than needed for their function (Pizzi and Frontali, 2001; Cristillo et al. 2001; Forsdyke, 2002b; Xue and Forsdyke 2003).

We thank James Gerlach, Christopher Madill, Andrew Schramm and Scott Smith for advice and assistance. Jean Lobry and Daniel Chessel kindly made their paper available prior to publication. Access to the GCG suite of programs was provided by the Canadian Bioinformatics Resource (Halifax). Academic Press, Cold Spring Harbor Laboratory Press and Elsevier Science gave permissions for the inclusion of full-text versions of some of the cited papers in Forsdyke's web pages.

Barrette IH, McKenna S, Taylor DR, Forsdyke DR (2001) Introns resolve the conflict between base order-dependent stem-loop potential and the encoding of RNA or protein: further evidence from overlapping genes. Gene 270:181-189

Bell SJ, Forsdyke DR (1999a) Accounting units in DNA. J Theor Biol 197:51-61

Bell SJ, Forsdyke DR (1999b) Deviations from Chargaff's second parity rule correlate with direction of transcription. J Theor Biol 197:63-76

Bernardi G, Bernardi G (1986) Compositional constraints and genome evolution. J Mol Evol 24:1-11

Bernardi G (2000) Isochores and the evolutionary genomics of vertebrates. Gene 241:3- 17

Cambillau C, Claverie J-M (2000) Structural and genomic correlates of hyperthermostability. J Biol Chem 275:32383-32386

Cantor CR, Schimmel PR (1980) Statistical mechanics and kinetics of nucleic acid interactions. In: Biophysical Chemistry. WH Freeman, San Francisco, pp. 1183- 1264

Cristillo AD, Mortimer JR, Barrette IH, Lillicrap TP, Forsdyke DR (2001) Double-stranded RNA as a not-self alarm signal: to evade, most viruses purine-load their RNAs, but some (HTLV-1, EBV) pyrimidine-load. J Theor Biol 208:475-491

Dalgaard JZ, Garrett A (1993) Archaeal hyperthermophile genes. In: Kates M, Kushner DJ, Matheson AT (eds) The Biochemistry of Archaea (Archaebacteria), Elsevier, Amsterdam, pp. 535-562

D'Onofrio G, Jabbari K, Musto H, Bernardi G (1999) The correlation of protein hydropathy with the base composition of coding sequences. Gene 238:3-14

Eigen M, Schuster P (1978) The hypercycle. A principle of natural self-organization. Part C. The realistic hypercycle. Naturwissenschaften 65:341-369

Forsdyke DR (1995) Entropy-driven protein self-aggregation as the basis for self/not- self discrimination in the crowded cytosol. J Biol Sys 3:273-287

Forsdyke DR (1996) Different biological species "broadcast" their DNAs at different (C+G)% "wavelengths". J Theor Biol 178:405-417

Forsdyke DR (1998) An alternative way of thinking about stem-loops in DNA. A case study of the G0S2 gene. J Theor Biol 192:489-504

Forsdyke DR (1999) Two levels of information in DNA. Relationship of Romanes' "intrinsic" variability of the reproductive system, and Bateson's "residue", to the species-dependent component of the base composition, (C+G)%. J Theor Biol 201: 47-61

Forsdyke DR (2001a) The Origin of Species, Revisited. McGill-Queen's University Press, Montreal

Forsdyke DR (2001b) Functional constraint and molecular evolution. In: Nature Encyclopedia of Life Sciences, Vol. 7. Nature Publishing Group, London, pp. 396-403

Forsdyke DR (2002a) Symmetry observations in long nucleotide sequences. Bioinformatics 18:215-217

Forsdyke DR (2002b) Selective pressures that decrease synonymous mutations in Plasmodium falciparum. Trends Parasitol 18:411-418

Forsdyke DR, Mortimer JR (2000) Chargaff's Legacy. Gene 261:127-137

Forterre P, Elie C (1993) Chromosome structure, DNA topoisomerases, and DNA polymerases in archaebacteria (archaea). In: Kates M, Kushner DJ, Matheson AT (eds) The Biochemistry of Archaea (Archaebacteria). Elsevier, Amsterdam, pp. 325-345

Fukuchi S, Nishikawa K (2001) Protein surface amino acid compositions distinctively differ between thermophilic and mesophilic bacteria. J Mol Biol 309:835-843

Galtier N, Lobry JR (1997) Relationships between genomic G+C content, RNA secondary structures, and optimal growth temperature in prokaryotes. J Mol Evol 44:632-636

Grantham R (1980) Workings of the genetic code. Trends Biochem Sci 5:327-331

Grove A, Lim L (2001) High affinity DNA binding of HU protein from the hyperthermophile Thermotoga maritime. J Mol Biol 311: 491-502

Hurst LD, Merchant AR (2001) High guanine-cytosine content is not an adaptation to high temperature: a comparative analysis among prokaryotes. Proc R Soc Lond B 268:493-497

Jaenicke R, Bohm G (1998) The stability of proteins in extreme environments. Curr Opin Struct Biol 8:738-748

Jenkins JM, Pagel M, Gould EA, Zanotto PM de A, Holmes EC (2001) Evolution of base composition and codon usage bias in the genus Flavivirus. J Mol Evol 52:383-390

Knight RD, Freeland SJ, Landweber LF (2001) A simple model based on mutation and selection explains trends in codon and amino-acid usage and GC composition within and across genomes. Genome Biol. 2:0010.1-0010.13.

Lao PJ, Forsdyke DR (2000) Thermophilic bacteria strictly obey Szybalski's transcription direction rule and politely purine-load RNAs with both adenine and guanine. Genome Res 10:228-236

Lauffer MA (1975) Entropy-Driven Processes in Biology. Springer-Verlag, New York

Lobry JR, Chessel D (2003) Internal correspondence analysis of codon and amino-acid usage in thermophilic bacteria. J Appl Genet 44:235-261.

Mortimer JR, Forsdyke DR (2003) Comparison of responses by bacteriophage and bacteria to pressures on the base composition of open reading frames. Appl. Bioinformatics 2:47-62.

Nakamura Y, Gojobori T, Ikemura T (2000) Codon usage tabulated from the international DNA sequence databases: status for the year 2000. Nucleic Acids Res 28:292

Pizzi E, Frontali C (2001) Low-complexity regions in Plasmodium falciparum proteins. Genome Res. 11:218-229

Ream RA, Johns GC, Somero GN (2003) Base compositions of genes encoding α-actin and lactate dehydrogenase-A from differently adapted vertebrates show no temperature-adaptive variation in G + C content. Mol Biol Evol 20:105-110

Saccone C, Gissi C, Lanave C, Larizza A, Pesole G, Reyes A (2000) Evolution of the mitochondrial genetic system: an overview. Gene 261:153-159

Shepherd JCW (1981) Method to determine the reading frame of a protein from the purine/pyrimidine genome sequence and its possible evolutionary justification. Proc Natl Acad Sci USA 78:1596-1600

Sicot F-X, Mesnage M, Masselot M, Exposito J-Y, Garrone R, Deutsch J, Gaill F (2000) Molecular adaptation to an extreme environment: origin of the thermal stability of the Pompeii worm collagen. J Mol Biol 302:811-820

Smithies O, Engels WR, Devereux JR, Slightom JL, Chen S-h (1981) Base substitutions, length differences and DNA strand asymmetries in the human G_g and A_g fetal globin gene region. Cell 26:345-353

Stetter KO (1999) Extremophiles and their adaptation to hot environments. F E B S Lett 452:22-25

Szybalski W, Kubinski H, Sheldrick O (1966) Pyrimidine clusters on the transcribing strand of DNA and their possible role in the initiation of RNA synthesis. Cold Spring Harb Symp Quant Biol 31:123-127

Xue HY, Forsdyke, DR (2003) Low complexity segments in Plasmodium falciparum proteins are primarily nucleic acid level adaptations. Mol. Biochem. Parasitol. 128:21-32