Symmetry observations in long nucleotide sequences
It followed from Chargaff's second parity rule for single bases (%A approximately equals %T; %G approximately equals %C for single strands of DNA), that this was likely to hold also for groups of two bases (2-tuples), three bases (3-tuples), and higher-tuple values. When a substantial number of long genomic sequences became available, V. V. Prabhu was able to demonstrate this very elegantly in 1993 (see below). The work was confirmed and extended by Forsdyke (1995; click here), and by Qi and Cuticchia (2001; see commentary below). It turned out that, had we been smart enough, we might have deduced all this from elementary principles decades earlier! Donald Forsdyke |
Symmetry observations in long nucleotide sequences
|
Vinayakumar V. Prabhu National Center for Biotechnology Information, National Institutes of Health, Bethesda, MD, USANucleic Acids Research, 1993, 21, 2797-2800Reproduced with the permission of V. V. Prabhu and the copyright holder Oxford University Press (Click Here). Received May 3, 1993; Accepted May 14, 1993
|
 |
A study of all sequences longer than 50000 nucleotides currently in GenBank (1, 2 ) reveals a simple symmetry principle. The number of occurrences of each n-tuple of nucleotides on a given strand approaches that of its complementary n-tuple on the same strand. This symmetry is true for all long sequences at small n (e.g. n = 1,2,3,4,5). It extends to sets of n-tuples of higher order n with increase in the length of the sequence.Table 1 lists all 32 sequences in GenBank longer than 50000 nucleotides. In all of these sequences, we find that the number of adenines approaches the number of thymines, and the number of guanines approaches that of cytosines on the same strand. |
| Table 1 | ||||||
| GenBank Code | Brief sequence description | Length | A | T | G | C |
| . | ||||||
|
YSCCHRIII |
Yeast chromosome III (cg) |
315357 |
98199 |
95609 |
59341 |
62208 |
|
HSSHCMVCG |
Human cytomegalovirus (cg) |
229354 |
49475 |
48776 |
66192 |
64911 |
|
VACCG |
Vaccinia virus (cg) |
191737 |
63921 |
63776 |
32030 |
32010 |
|
MPOMTCG |
Liverwort mitochondrion (cg) |
186608 |
53206 |
54264 |
39924 |
39214 |
|
HS4B958RAJ |
Epstein-Barr virus |
184113 |
36002 |
37665 |
54622 |
55824 |
|
HS4 |
Epstein-Barr virus (cg) |
172282 |
34054 |
34962 |
50755 |
52511 |
|
TOBCPCG |
Nicotiana tabacum chloroplast (cg) |
155844 |
47824 |
49037 |
28992 |
29991 |
|
(a) |
Caenorbabditis elegans segment 1 |
152850 |
49947 |
48870 |
27764 |
26269 |
|
HS11CG |
Herpes simplex virus 1 (cg) |
152260 |
24241 |
24051 |
52510 |
51458 |
|
HSECOMGEN |
Equine herpesvirus I (cg) |
150223 |
32616 |
32482 |
41952 |
43173 |
|
RICCPOSXX |
Rice chloroplast genome |
134525 |
41248 |
40831 |
26320 |
26126 |
|
IH1CG |
Channel catfish virus (cg) |
134226 |
28727 |
30026 |
37707 |
37766 |
|
HS3CG |
Varicella-Zoster virus (cg) |
124884 |
33789 |
33623 |
28177 |
29295 |
|
MPOCPCG |
Liverwort chloroplast (cg) |
121024 |
42896 |
43263 |
17556 |
17309 |
|
ECOMORI |
Escherichia coli segment 1 |
111402 |
26086 |
26742 |
30524 |
28050 |
|
HSIULR |
Herpes simplex virus 1 long region |
108360 |
18038 |
17836 |
36792 |
35694 |
|
HUMNEUROF |
Human neurofibromatosis 1 exons |
100849 |
30346 |
32481 |
19387 |
18635 |
|
PANMTPACGA |
Podspora anserina mitochondrion |
100314 |
35804 |
34358 |
16724 |
13428 |
|
HUMTCRADCV |
Human T-cell receptor genes |
97634 |
28063 |
26384 |
22236 |
20951 |
|
MUSTCRA |
Mouse T-cell receptor locus |
94647 |
26359 |
25769 |
21729 |
20790 |
|
ECOUW85U |
E. coli segment 2 |
91408 |
21251 |
22107 |
24848 |
23089 |
|
DROABDB |
Drosophila melanogaster gene |
80423 |
23439 |
23596 |
16641 |
16747 |
|
YSCMTCG |
Yeast mitochondrion (cg) |
78521 |
32880 |
31633 |
7350 |
6432 |
|
(b) |
C. elegans segment 2 |
75821 |
25658 |
24097 |
13320 |
12746 |
|
HUMHBB |
Human 6 -globin on chromosome 11 |
73326 |
22072 |
22293 |
14789 |
14169 |
|
EPFCPCG |
Epifagus virginiana chloroplast (cg) |
70028 |
21885 |
22934 |
12448 |
12761 |
|
HUMMMDBC |
Human chromosome 19 segment |
68505 |
15961 |
16482 |
18410 |
17646 |
|
HUMGHCSA |
Human growth hormone genes |
66495 |
17311 |
16472 |
16441 |
16271 |
|
HUMHDABCD |
Human chromosome 4 segment |
58864 |
13422 |
14690 |
15906 |
14846 |
|
HUMHPRTB |
Human gene (Lesch-Nyhan synd) |
56737 |
15689 |
18168 |
11599 |
11281 |
|
MUSBGCXD |
Mouse beta-globin |
55856 |
17154 |
16457 |
11381 |
10864 |
|
RATCRYG |
Rat gamma-crystallin cluster |
54670 |
14414 |
14443 |
10906 |
11628 |
| Abbreviation
used: (cg), complete genome
(a) Concatenation of cosmids CEL1, CELZK643, CELZK638, CELR08D7 and CELF59B2. (b) Concatenation of cosmids CELB0303 and CELZK370. |
||||||
Table 2 shows the number of occurrences of all complementary pairs of 2-tuples and 3-tuples for four sequences from Table 1. The complement of a tuple is taken in the opposite direction of that tuple. Thus the complement of ACG is CGT (not TGC). One notes that each 2,3-tuple on a given strand tends to approach the same number of occurrences as its complementary tuple on the same strand. This tendency is general to all sequences of Table 1. While this symmetry is found true for overlapping and nonoverlapping tuples, the figures and tables of this report are for overlapping tuples only. For example, the sequence ACGCT has as overlapping 3-tuples ACG, CGC, GCT. Palindromic tuples, such as AT, TA, GC, CG, ACGT etc. are excluded from the tables and figure since the tuples are identical to their complements. |
| Table 2 | |||||||||
|
. |
. |
VACCG |
(192 k) |
RICCPOSXX |
(135 k) |
MPOCPCG |
(121 k) |
DROABDB |
(80 k) |
|
AA |
TT |
20360 |
20339 |
14756 |
14480 |
18566 |
18963 |
8537 |
8573 |
|
AG |
CT |
10265 |
10084 |
8203 |
8099 |
5978 |
5964 |
4136 |
4036 |
|
AC |
GT |
10183 |
10241 |
6037 |
6001 |
5104 |
5087 |
3967 |
4188 |
|
TG |
CA |
10504 |
10687 |
7087 |
7162 |
5855 |
5774 |
5255 |
5262 |
|
TC |
GA |
12239 |
12180 |
9034 |
9100 |
5688 |
5800 |
4492 |
4364 |
|
GG |
CC |
5340 |
5319 |
6654 |
6489 |
3543 |
3391 |
3742 |
3941 |
|
AAA |
TTT |
7365 |
7416 |
5586 |
5408 |
8820 |
9005 |
3346 |
3407 |
|
AAT |
ATT |
6646 |
6702 |
4180 |
4158 |
5387 |
5592 |
2514 |
2460 |
|
AAG |
CTT |
2930 |
2831 |
2932 |
2920 |
2277 |
2307 |
1364 |
1306 |
|
AAC |
GTT |
3418 |
3390 |
2058 |
1994 |
2082 |
2058 |
1313 |
1400 |
|
ATA |
TAT |
7784 |
7710 |
3374 |
3366 |
4355 |
4453 |
1816 |
1832 |
|
ATG |
CAT |
4059 |
4190 |
2155 |
2201 |
1675 |
1727 |
1406 |
1426 |
|
ATC |
GAT |
4567 |
4566 |
2564 |
2504 |
1625 |
1681 |
1117 |
1027 |
|
AGA |
TCT |
4539 |
4455 |
2992 |
2954 |
1929 |
1898 |
1137 |
1139 |
|
AGT |
ACT |
2998 |
2989 |
1843 |
1834 |
1648 |
1670 |
1120 |
1087 |
|
AGG |
CCT |
1457 |
1405 |
1916 |
1882 |
1186 |
1139 |
769 |
771 |
|
AGC |
GCT |
1271 |
1235 |
1452 |
1429 |
1215 |
1257 |
1110 |
1039 |
|
ACA |
TGT |
3585 |
3600 |
1629 |
1601 |
1668 |
1590 |
1370 |
1523 |
|
ACG |
CGT |
2051 |
2020 |
1015 |
1000 |
697 |
680 |
730 |
790 |
|
ACC |
GGT |
1558 |
1622 |
1559 |
1557 |
1069 |
1169 |
780 |
755 |
|
TAA |
TTA |
6001 |
5998 |
2803 |
2812 |
4874 |
5041 |
1931 |
1926 |
|
TAG |
CTA |
3593 |
3436 |
2240 |
2213 |
1822 |
1798 |
675 |
685 |
|
TAC |
GTA |
3390 |
3476 |
1820 |
1831 |
1607 |
1562 |
838 |
849 |
|
TTG |
CAA |
3163 |
3260 |
2651 |
2698 |
2490 |
2411 |
1664 |
1639 |
|
TTC |
GAA |
3762 |
3734 |
3609 |
3669 |
2427 |
2461 |
1576 |
1621 |
|
TGA |
TCA |
3298 |
3430 |
2189 |
2176 |
1871 |
1789 |
1217 |
1215 |
|
TGG |
CCA |
2226 |
2234 |
1975 |
1997 |
1363 |
1275 |
1225 |
1370 |
|
TGC |
GCA |
1380 |
1438 |
1322 |
1360 |
1031 |
1042 |
1290 |
1307 |
|
TCG |
CGA |
1990 |
1973 |
1566 |
1576 |
739 |
745 |
1050 |
995 |
|
TCC |
GGA |
2364 |
2370 |
2338 |
2343 |
1262 |
1255 |
1087 |
1014 |
|
GAG |
CTC |
2076 |
2105 |
1792 |
1752 |
946 |
922 |
945 |
978 |
|
GAC |
GTC |
1804 |
1805 |
1135 |
1109 |
112 |
714 |
771 |
821 |
|
GTG |
CAC |
1570 |
1571 |
1067 |
1024 |
753 |
703 |
1118 |
1045 |
|
GGG |
CCC |
612 |
625 |
1745 |
1589 |
589 |
581 |
889 |
970 |
|
GGC |
GCC |
736 |
772 |
1009 |
1002 |
530 |
479 |
1084 |
1104 |
|
GCG |
CGC |
824 |
882 |
774 |
782 |
348 |
350 |
897 |
863 |
|
CAG |
CTG |
1666 |
1712 |
1239 |
1214 |
933 |
937 |
1152 |
1067 |
|
CGG |
CCG |
1045 |
1055 |
1018 |
1021 |
405 |
396 |
859 |
830 |
Figure 1 displays the number of occurrences of complementary 4-tuple and 5-tuple pairs for the four sequences of Table 2. The straight line in each frame is of slope 1. Each dot in a frame represents one complementary tuple pair, and its (X,Y) coordinates are the (number of occurrences of the tuple, number of occurrences of its complementary tuple) on the same strand of the sequence. Each frame on the left contains all 120 complementary 4-tuple pairs, while that on the right includes all 512 complementary 5-tuple pairs in the sequences labelled. The dots agglutinate at the line of slope 1, demonstrating that the number of occurrences for all 4,5-tuples approaches that of their complements. For the entire set of dots in any frame of Figure 1, one can calculate two statistical measures (r, m) (3, 4) that characterise the symmetry. r, the correlation coefficient, is close to 1.0 for sets in which complementary members of each tuple pair are correlated (but not necessarily symmetric). m is the slope of the least squares fitted line. Both r and m approach 1.0 for sets in which members of each tuple pair are not merely correlated but also are symmetric. |
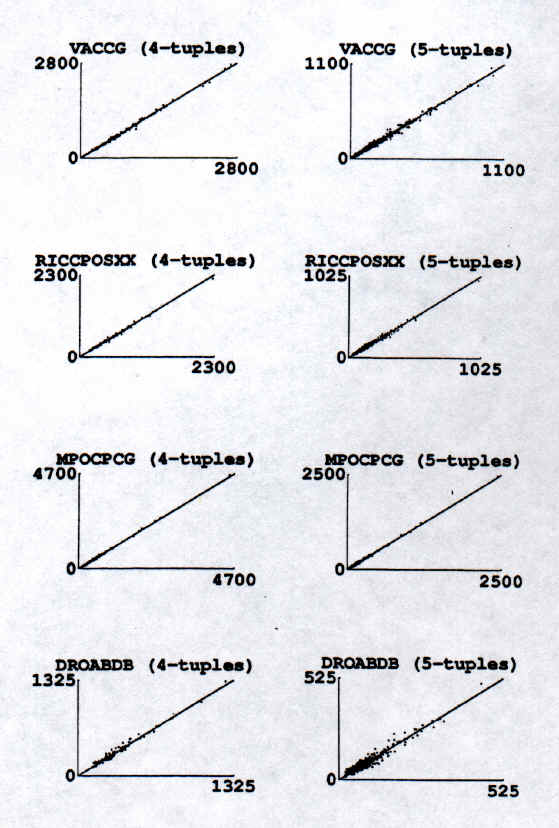 |
Figure 1. The straight line in each frame is of unit slope. Each dot represents a complementary tuple pair and has for (X, Y) coordinates, the number of occurrences of (tuple, complementary tuple). The dots agglutinate around the line of unit slope showing that the number of occurrences of each tuple approaches that of its complementary tuple on the same strand of the sequence. |
Table 3 illustrates concisely the symmetry in sets of complementary pairs of 3, 4, 5, 6-tuples in all sequences of Table 1. One notices from Table 3 that for each sequence the correlation coefficients diminish with increase in the order of the tuple. A statistical occurrence of tuples appears to be required before the symmetry is manifest (4, 5, 6), although correlations and tendencies towards symmetry are evident in some sequences even a 1000 bases long. |
| Table 3 | ||||||||
| . | 3-tuples | 4-tuples | 5-tuples | 6-tuples | ||||
| . | r | m | r | m | r | m | r | m |
|
YSCCHRIII |
0.989 |
0.933 |
0.985 |
0.943 |
0.98 0 |
0.946 |
0.963 |
0.93 0 |
|
HS5HCMVCG |
0.987 |
0.957 |
0.979 |
0.976 |
0.972 |
0.955 |
0.945 |
0.927 |
|
VACCG |
0.999 |
0.997 |
0.998 |
1.001 |
0.995 |
0.992 |
0.983 |
0.992 |
|
MPOMTCG |
0.991 |
1.112 |
0.983 |
1.093 |
0.974 |
1.063 |
0.948 |
1.03 0 |
|
H$4B958RAJ |
0.966 |
1.022 |
0.948 |
1.035 |
0.93 |
0.993 |
0.854 |
0.904 |
|
HS4 |
0.96 |
1.045 |
0.942 |
1.056 |
0.922 |
1.007 |
0.848 |
0.917 |
|
TOBCPCG |
0.992 |
0.996 |
0.989 |
1.018 |
0.983 |
1.024 |
0.968 |
1.013 |
|
(a) |
0.995 |
0.98 0 |
0.992 |
0.986 |
0.986 |
0.985 |
0.968 |
0.975 |
|
HSIICG |
0.998 |
0.962 |
0.996 |
0.962 |
0.993 |
0.965 |
0.982 |
0.953 |
|
HSECOMGEN |
0.977 |
1.024 |
0.965 |
1.011 |
0.949 |
0.969 |
0.892 |
0.895 |
|
RICCPOSXX |
0.999 |
0.986 |
0.997 |
0.988 |
0.989 |
0.976 |
0.97 |
0.961 |
|
IHICG |
0.989 |
0.97 0 |
0.975 |
0.974 |
0.948 |
0.974 |
0.863 |
0.876 |
|
HS3CG |
0.959 |
0.987 |
0.944 |
0.95 |
0.925 |
0.907 |
0.858 |
0.837 |
|
MPOCPCG |
1 .000 |
1.03 0 |
0.999 |
1.018 |
0.997 |
1.007 |
0.993 |
1.005 |
|
ECOMORI |
0.893 |
0.822 |
0.883 |
0.799 |
0.875 |
0.856 |
0.828 |
0.777 |
|
HSIULR |
0.994 |
0.941 |
0.988 |
0.939 |
0.981 |
0.941 |
0.956 |
0.919 |
|
HUMNEUROF |
0.974 |
1.059 |
0.968 |
1.04 0 |
0.955 |
0.996 |
0.923 |
0.927 |
|
PANMTPACGA |
0.968 |
0.944 |
0.957 |
0.93 |
0.954 |
0.925 |
0.928 |
0.897 |
|
HUMTCRADCV |
0.96 0 |
0.854 |
0.945 |
0.871 |
0.927 |
0.856 |
0.876 |
0.799 |
|
MUSTCRA |
0.977 |
0.936 |
0.964 |
0.923 |
0.943 |
0.915 |
0.894 |
0.854 |
|
ECOUW85U |
0.842 |
0.752 |
0.831 |
0.758 |
0.819 |
0.771 |
0.756 |
0.717 |
|
DROABDB |
0.994 |
1.009 |
0.986 |
1.002 |
0.967 |
0.974 |
0.911 |
0.934 |
|
YSCMTCG |
0.998 |
0.939 |
0.994 |
0.933 |
0.995 |
0.908 |
0.989 |
0.866 |
|
(b) |
0.989 |
0.924 |
0.986 |
0.923 |
0.978 |
0.931 |
0.958 |
0.92 0 |
|
HUMHBB |
0.99 0 |
1.034 |
0.984 |
1.016 |
0.966 |
0.992 |
0.916 |
0.931 |
|
EPFCPCG |
0.99 0 |
1.112 |
0.987 |
1.146 |
0.98 0 |
1.123 |
0.968 |
1.134 |
|
HUMMMDBC |
0.978 |
0.946 |
0.972 |
0.976 |
0.958 |
0.978 |
0.929 |
0.953 |
|
HUMGHCSA |
0.97 0 |
0.924 |
0.937 |
0.921 |
0.878 |
0.838 |
0.757 |
0.74 0 |
|
HUMHDABCD |
0.922 |
0.922 |
0.924 |
0.932 |
0.913 |
0.93 0 |
0.874 |
0.897 |
|
HUMHPRTB |
0.919 |
1.261 |
0.902 |
1.221 |
0.888 |
1.144 |
0.851 |
1.074 |
|
MUSBGCXD |
0.974 |
0.915 |
0.952 |
0.929 |
0.93 0 |
0.849 |
0.839 |
0.835 |
|
RATCRYG |
0.978 |
0.967 |
0.962 |
0.977 |
0.922 |
0.924 |
0.822 |
0.805 |
The ratio of sequence length to the number of possible kinds of n-tuples decreases with increasing tuple order. For example, in the yeast sequence YSCCHRIII the length/tuple ratio is 315357/16 for doublets but 315357/4096 for 6-tuples. The occurrence of each 6-tuple is restricted to a greater degree by the sample length than the doublets. This reflects as a gradual broadening of the cluster with tuple order in Figure 1. Since the number of occurrences of each n-tuple approaches that of its complement on the same strand, a given n-tuple tends to have the same number of occurrences on both the complementary strands of long DNA sequences. The two complementary strands of long DNA sequences, therefore, approach having the same numerical distribution of n-tuples in those n for which the symmetry is valid. A tendency towards attaining such equivalence between complementary strands may, perhaps, be causing the observed symmetry on each of the two strands. ACKNOWLEDGEMENTS The author thanks Dr David J. Lipman and Dr W. John Wilbur for suggesting relationship of data to strand equivalence and Dr. J. -M. Claverie for suggesting scatter plots to present the data. REFERENCES 1. Bilofsky,H.S. and Burks,C., (1988) Nucleic Acids Res., 16, 1861-1863. 2. GenBank (74.0) ; NewGenBank (74.0+, 31 December 1992). 3. Neter, J., Wasserman, W. and Kutner, M. H. (1985) Applied linear statistical models. Ed. 2, Richard D. Irwin, Inc., Homewood, IL., 502-504. 4. Fickett, J. W., Tomey, D. C. and Wolf, D. R. (1992) Genomics 13, 1056-1064. 5. Kozhukhin, C. G. and Pevzner, P. A. (1991) Comp. Appl. Biosci. 7, 39-49. 6. Pevzner,P.A. (1992) Computers Chem. 16, No. 2, 103-106. |
| Symmetry
observations in long nucleotide sequences: a commentary on the Discovery
Note of Qi and Cuticchia [Bioinformaticists rediscover biochemists' wheels] Bioinformatics
(2002) 18, 215-217 D. R. Forsdyke Reverse and Forward Complements Randomization Removes Base-Order-Dependent Correlations "Discovery Note" of Qi and Cuticchia
In 1993 Prahbu began a paper entitled "Symmetry observations in long nucleotide sequences" with the concise and elegant statement:
Since the sequences were from 22 species from a wide range of taxa the symmetry principle appeared broadly applicable. Prabhu demonstrated the principle by plotting the frequencies of oligonucleotides of a given length (n) against the frequencies of their corresponding complement (Alff-Steinberger, 1987). Since the frequencies were similar, the plots were rectilinear with a slope of 1.0 and intersected the origin. The correlation coefficient (r) provided a measure of the extent to which the DNA of a particular species followed the principle. For example, for most species r-values for 6-tuples approached unity (0.8-1.0), but a 111 kb segment from E. coli fell below this range (0.76). In his brief paper Prabhu (1993) did not distinguish the contributions of base composition and base order by comparing natural sequences with sequences randomized to destroy the natural order of bases (Yomo and Ohno, 1989). Furthermore, he did not refer to previous work in the area, and did not suggest a functional basis for the symmetry principle. In 1995 Forsdyke presented a more extensive discussion of the phenomenon, which appeared to relate to the long known second parity rule of Chargaff; namely, that for long single strands of DNA the Watson-Crick pairing bases are present in approximately equal frequencies (%A = %T; %G = %C). In 1984 Nussinov had suggested a function related to "advantageous DNA structure." Blake and Hinds, (1984) had suggested a function related to RNA structure. Forsdyke's data (1995) were consistent with the hypothesis that the ability of duplex DNA to extrude stem-loops would be advantageous for recombination, so that mutations favoring this (i.e. mutations favoring equifrequencies of the Watson-Crick bases in single strands) would confer a selective advantage (Bell and Forsdyke, 1999a, b; Forsdyke and Mortimer, 2000). Reverse and Forward Complements Since, by convention, the sequence of a nucleic acid is written from the 5' end to the 3' end, and since the complementary ("bottom") strand of a double helix runs in the opposite direction to that of the "top" strand, the complement of, for example, the trinucleotide CAT, would be ATG in the bottom strand. The latter can be referred to as the "reverse complement" to distinguish it from "GTA" in the bottom strand (written in this particular instance in the 3' to 5' direction), which can be referred to as the corresponding "forward complement." This triplet, when occurring normally elsewhere in DNA, would be written in the 5' to 3' direction, and then its complement ("reverse complement") would be TAC. The above Nussinov-Forsdyke hypothesis requires a selection pressure on the base-order of a natural sequence favoring the generation in the same strand of equifrequencies of reverse complements (i.e. CAT matching ATG), but not of equifrequencies of sequences corresponding to forward complements (i.e. CAT not matching GTA). For this we must invoke another rule. Sequences corresponding to forward complements appear to exist independently of each other in the same DNA strand. However, a factor supporting correlation in this case would be the genome-wide pressure favoring uniformity of base composition within a species (GC%; Chargaff, 1951; Wyatt, 1952; Forsdyke and Mortimer, 2000). This is because a sequence (e.g. CAT) and both its reverse and its forward complements (e.g. ATG and GTA) have the same base composition when this is expressed as GC% (e.g. 67% A+T; 33% G+C). Thus, there should be some matching between the frequencies of oligonucleotide sequences (e.g. CAT) and of sequencies corresponding to their forward complement (e.g. GTA), in the same DNA strand. Randomization Removes Base-Order-Dependent Correlations In summary, evolutionary pressures on both the order and the composition (GC%) of bases in oligonucleotides work to favor the equifrequency of oligonucleotides and their reverse complements in the same DNA strand. Evolutionary pressures on base composition (GC%) alone, work to favor the equifrequency of oligonucleotides and their forward complements (when the latter, written in the 5' to 3' direction, appear elsewhere in the same DNA strand). Hence, in natural sequences, but not in sequences artificially randomized to eliminate evolutionary effects on base order, correlations between oligonucleotides and their reverse complements should be better than correlations between oligonucleotides and their forward complements. In terms of the above trinucleotide pairs, the difference between the frequencies of CAT and ATG should be low, whereas the difference between the frequencies of CAT and GTA should be high. Whereas in prokaryotes and lower eukaryotes base compositions tend to be uniform genome-wide, in higher eukaryotes genomes are segmented into isochores each with a distinct base composition. Depending on the size of the segment under study, this could further work to diminish the correlation between the frequencies of oligonucleotides and their forward complements in single-stranded DNA. "Discovery Note" of Qi and Cuticchia Using the same methods as Prabhu (1993) and Forsdyke (1995), in a note entitled "Compositional symmetries in complete genomes" Qi and Cuticchia (2001) have presented data bearing on the above. Hinting at biological relevance, their direct quotations from Bell and Forsdyke (1999a) include the suggestion that Chargaff's second parity rule reflects the evolution "of genome-wide stem-loop potential as part of short- and long-range accounting processes which work together to sustain the integrity of various levels of information in DNA." There are five main observations:
The first three of these observations represent an affirmation of previous reports of work performed using some complete, but mainly incomplete genomic sequences. The last two observations, deducible from the above first principles, could have been made using incomplete sequences. At least with regard to the issues considered here, there appears little need for complete genomic sequences (Forsdyke, 2001a). Indeed, many modern inferences derive from biochemical studies made decades before direct counting of individual bases became feasible [see G. Bernardi 2001. Gene 2001; 276, 3-13]. The biological implications of oligonucleotide symmetry are considered more fully elsewhere (Forsdyke and Mortimer, 2000; Forsdyke, 2001b). References Alff-Steinberger, C. (1987) Codon usage in Homo sapiens: evidence for a coding pattern on the non-coding strand and evolutionary implications of dinucleotide discrimination. J. Theor. Biol., 124, 89-95. Bell, S. J. and Forsdyke, D. R. (1999a) Accounting units in DNA. J. Theor. Biol., 197, 51-61. (Click Here) Bell, S. J. and Forsdyke, D. R. (1999b) Deviations from Chargaff's second parity rule correlate with direction of transcription. J. Theor. Biol. 197, 63-76. (Click Here) Blake, R. D. and Hinds, P. W. (1984) Analysis of codon bias in E. coli sequences. J. Biomol. Struct. 2, 593-606. Chargaff, E. (1951) Structure and function of nucleic acids as cell constituents. Fed. Proc. 10, 654-659. Forsdyke, D. R. (1995) Relative roles of primary sequence and (G+C)% in determining the hierarchy of frequencies of complementary trinucleotide pairs in DNAs of different species. J. Mol. Evol. 41, 573-581. (Click Here) Forsdyke, D. R. (2001a) Did Celera invent the internet? Lancet 357, 1203. (Click Here) Forsdyke, D. R. (2001b) The Origin of Species, Revisited. McGill-Queen's University Press, Montreal. (Click Here) Forsdyke, D. R. and Mortimer, J. R. (2000) Chargaff's legacy. Gene 261, 127-137. (Click Here) Nussinov, R. (1984) Strong doublet preferences in nucleotide sequences and DNA geometry. J. Mol. Evol., 20, 111-119. Prabhu, V. V. (1993) Symmetry observations in long nucleotide sequences. Nucleic Acids Res., 21, 2797-2800. Qi, D. and Cuticchia, A. J. (2001) Compositional symmetries in complete genomes. Bioinformatics 17, 557-559. Wyatt, G. R. (1952) The nucleic acids of some insect viruses. J. Gen. Physiol. 36, 201-205. Yomo, T. and Ohno, S. (1989) Concordant evolution of coding and non-coding regions of DNA made possible by the universal rule of TA/CG deficiency - TG/CT excess. Proc. Natl. Acad. Sci. USA 86, 8452-8456. [See also Ohno, S. 1991. The grammatical rule of DNA language: messages in palindromic verses. In Evolution of Life. Edited by S. Osawa and T. Honjo. Springer-Verlag.] |
Go to: Trinucleotide Hierarchies (1995) (Click Here)
Go to: Elementary Principles (2004) (Click Here)
Return to: Bioinformatics/Genomics Index (Click Here)
Return to: Evolution Index (Click Here)
Return to: Peer Review Index (Click Here)
Return to: HomePage (Click Here)
This page was established circa 2000 and last edited on 11 November 2020 by Donald Forsdyke